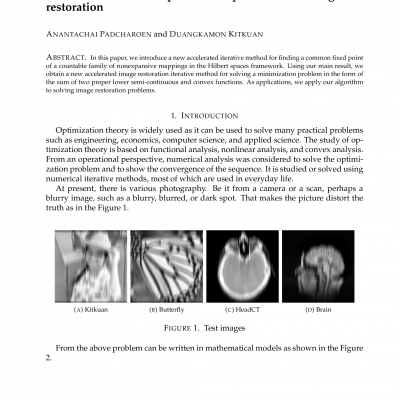
carpathian_2024_40_3_655_679In real Hilbert spaces, given a single-valued Lipschitz continuous and monotone operator, we study generalized split feasibility problem (GSFP) over solution set of monotone variational inclusion problem. An inertia iterative method is proposed to solve this problem, by showing that the sequence generated by the iteration converges strongly to solution of GSFP. As against previous methods, our step size is chosen to be simple and not depending on norm of associated bounded linear map as well as Lipschitz constant of the single-valued operator. The obtained result was applied to study split linear inverse problem, precisely, the LASSO problem. Lastly, with the aid of numerical examples, we exhibited efficiency of our algorithm and its dominance over other existing schemes.
